| |
 融资租赁行业2023年回顾与2024年展望
联合资信主要观点:
2023年10月下发了金融租赁公司管理办法,体现了监管机构对
融资租赁行业2023年回顾与2024年展望
联合资信主要观点:
2023年10月下发了金融租赁公司管理办法,体现了监管机构对
 2023年租赁业调查报告(毕马威)
毕马威连续第5年发布租赁业调查报告。本刊结合租赁行业热点话题提供专业洞察,并汇总
2023年租赁业调查报告(毕马威)
毕马威连续第5年发布租赁业调查报告。本刊结合租赁行业热点话题提供专业洞察,并汇总
 2021年度融资租赁业调查报告
2021年度融资租赁业调查报告
下载地址:原链接
2021年度融资租赁业调查报告
2021年度融资租赁业调查报告
下载地址:原链接
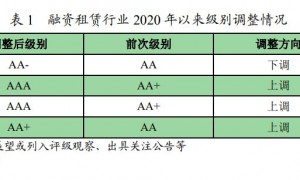 2021年融资租赁行业信用风险展望
一、融资租赁行业 2020 年信用风险回顾
1.信用等级迁移及风险事件回顾
202
2021年融资租赁行业信用风险展望
一、融资租赁行业 2020 年信用风险回顾
1.信用等级迁移及风险事件回顾
202
 《金融租赁行业发展报告(2007-2017)》
金融租赁行业发展报告(2007-2017)
《报告》主体内容分为导言、发展篇、环境篇、资产
《金融租赁行业发展报告(2007-2017)》
金融租赁行业发展报告(2007-2017)
《报告》主体内容分为导言、发展篇、环境篇、资产